Hypothesis Testing

Learning Objectives

1. Define and apply the various components of hypothesis testing, including: the null hypothesis, the research (or alternative) hypothesis, the test statistic and the critical statistic
2. Understand the significance of rejecting/failing to reject the null hypothesis
3. Carry out one- and two-group hypothesis tests

Key Terms

The null hypothesis (H0): a hypothesis that assumes there is no difference between the population parameters of the groups being tested. Under this assumption, any apparent difference between sample statistics is the result of sampling error.
The research/alternative hypothesis (H1): a hypothesis that assumes the apparent difference between two sample statistics (or between a sample statistic and a population parameter) is due to actual differences in population parameters rather than sampling error. This hypothesis directly contradicts the null hypothesis (if the research hypothesis is true, the null must be false, and vice versa). Often researchers get excited when the research hypothesis proves to be correct.
Alpha level (α): the level of probability at which the null hypothesis is rejected. In the social sciences, we usually set the alpha level at 0.05.

The t Distribution

The t Distribution is actually a series of distributions where the exact shape of each is determined by its respective degrees of freedom. The degrees of freedom represent the number of scores that are free to vary in calculating each statistic. For our purposes today, we can calculate the degrees of freedom by subtracting one from the total number of observations in each sample. So, the number of degrees of freedom will be nearly the same as the number of observations.

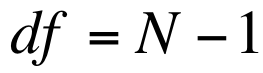
With few degrees of freedom, the t Distribution is very flat. As the degrees of freedom increase, the t Distribution looks more and more like the normal distribution. With 120+ degrees of freedom, it's indistinguishable from the normal distribution (and has all the same properties).

Hypothesis Testing and the t Distribution

This week we'll be talking about hypothesis tests as they apply to the means of two distributions. Sometimes that involves comparing a sample statistic to a population parameter (i.e., comparing the mean number of sexual partners in a sample of Sociology majors with the mean number of sexual partners of the entire student body), and sometimes it involves comparing the means of two samples (i.e., comparing the mean income of a sample of college graduates with the mean income of a sample of high school graduates). We can also do this for the proportions of two groups, but that process is slightly different than this one, so we will discuss it separately. What follows is a very general outline of hypothesis testing. For a more in-depth discussion, I highly recommend you read the chapter on hypothesis testing from David M. Lane's Online stats book.

Regardless of what we're testing, it's hard to be sure whether or not our data are indicative of a difference in the general population because of sampling error. In other words, the difference we're observing could have occurred simply by chance. In order to figure out just how unusual our results are, we run a hypothesis test. We often want our results to be unusual; the fact that the difference between two means (or two proportions) can't be explained by chance often means we've found some kind of noteworthy underlying pattern. There are lots of different kinds of hypothesis tests, but they all follow the same basic outline:

1. First we state our assumptions. There are certain criteria that need to be met before we can carry out a hypothesis test. These criteria will also determine which variety of hypothesis test we can use:

• Our sample must be randomly selected in order to minimize potential selection biases
• Our data must be interval/ratio (please don't try to carry out a t test on maleness or blackness or Mormon-ness)
• Our data must be normally distributed OR we must have a sample size of at least 50 for each group

2. Next we state our null/research hypotheses and set our alpha level.

• Our null hypothesis is always an equality, and it's usually the opposite of what we want to prove (some people like to think of it as being the status quo).
• Our research hypothesis is always an inequality, and it will determine what kind of test we use (i.e. one-tailed or two-tailed, which will be explained in more detail below).
• Our alpha level is our level of confidence for avoiding a Type One error. In other words, with an alpha of .05 (which is the most common in the social sciences), we're 95 percent sure we won't accidentally reject a true null hypothesis.

3. Third, we state our sampling distribution and our degrees of freedom and determine our critical statistic. Today, our sampling distribution is the difference between two means (i.e. the t Distribution) and our critical statistic is a t statistic. Playing with t statistics requires that we use a table not unlike the one for z statistics. Such a table is available on Canvas in the "Files" section. You'll note that the levels of significance are across the top and the degrees of freedom are along the side. The number that corresponds to a given level of significance and a certain number of degrees of freedom is what's known as a critical statistic. For example, the critical statistic for a one-tailed test with 60 degrees of freedom and an alpha of .05 is 1.671.

4. Fourth, we calculate our test statistic. We calculate a t-statistic in much the same way we would calculate a z statistic for a sampling distribution. The formulas for the one-group (comparing a sample mean to a population parameter) and two-group (comparing two sample means) hypothesis tests are as follows:

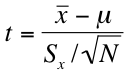
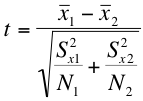
5. Finally, we accept or reject our null hypothesis. The absolute value of the obtained statistic must be larger than the critical statistic in order to reject the null hypothesis. We'll talk more about that below.

Hypothesis Testing with One Sample Mean

In this example, we're going to carry out a hypothesis test involving a single sample mean. In other words, we're going to see whether our sample mean is different from a known (or hypothesized) value. Let's say I'm testing a new diet drug that I believe dramatically increases weight loss. I know for a fact that the average person, via diet and exercise, will lose approximately two pounds per week. A sample of 100 people on my wonder drug, however, lost an average of three pounds per week with a standard deviation of one pound. Does my wonder drug work, or is the difference between my sample and the population entirely the result of sampling error?

First, we need to state our assumptions. Since this is my hypothetical example, it's safe to assume our data were randomly sampled. Weight (measured in pounds) is an interval/ratio variable, and we have a sample size greater than 50.

Next, we state our null and research hypothesis. Our null hypothesis is that my wonder drug doesn't work, and the mean of my sample is really no different from that of the population (in which case any apparent weight loss in the sample would have been due to dumb luck rather than the effectiveness of my wonder drug):

Our research hypothesis is that the drug does work, and the mean of my sample is greater than the mean of the population:

Because this research hypothesis specifies directionality (i.e. uses a "greater than" sign rather than a "not equal" sign), this will be a one-tailed test. For this test, let's set our alpha at 0.05. Now we calculate our t-statistic using the following formula:

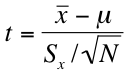
In other words, we subtract the known or hypothesized population mean from our sample mean and divide the result by the standard error of the mean. For the purposes of this problem, our equation would look like this:

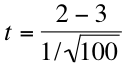
If we work that out, we get an obtained statistic of -10. When evaluating obtained against critical statistics, we're only interested in the absolute value of our obtained statistic. In order to make sense of that number, we need to compare it to the critical statistic from our table. First, however, we need to calculate our degrees of freedom, which are given by the formula N – 1 (100 – 1 = 99, so we have 99 degrees of freedom).

To use the table, find .05 in the "one-tail" line along the top of the table, and follow that column down to 99 degrees of freedom. You may notice at this point that 99 degrees of freedom is not included on our table. We have 80 and 100, but not 99. We want to get as close as we can without going over. With that in mind, we'd use the critical statistic found at 80 degrees of freedom, which is 1.664.

Finally, we compare our statistics and state our conclusion. If the absolute value of our obtained statistic is greater than the critical statistic, we can reject the null hypothesis. Because 10 is greater than 1.664 (the absolute value of -10 is 10), we can reject the null hypothesis and conclude that my wonder drug really works.

Hypothesis Testing with Two Sample Means

Now we're going to carry out a two-group hypothesis test using the following scores from a sample of men and women who took a standardized test:

Women: N = 41, Mean = 98, Standard Deviation = 8
Men: N = 21, Mean = 96.6, Standard Deviation = 12

Just from looking at the two sample means, we can see that women scored a little higher on this test than did men. But will that difference hold true for their respective populations, or is it due to sampling error? Let's find out.

First we state our assumptions. Since I'm giving you this example, I think it's safe to assume that the data was randomly selected and normally distributed. Test scores are definitely interval/ratio, so we can check that off as well.

Next, we state our null and research hypotheses and set our alpha level. Our null hypothesis is that the mean scores for the men and women who took this test are equal, so we would write something like this:

Our research hypothesis is that the means are not equal, so we would say:

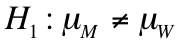
Because our research hypothesis is a simple inequality, we can run a two-tailed test. In other words, we don't care which mean is bigger than the other as long as they're not equal. If we wanted to prove that the mean score for women was higher than that of men, we would run a one-tailed test. As for our alpha level, we'll use 0.05 since it's usually the standard used in the social sciences.

Third, we state our sampling distribution, our degrees of freedom and calculate our critical statistic. We're testing the difference between two means, so our sampling distribution is the t distribution In this case our df is found by the equation (N-1)+(N-1), or 40 +20 = 60. If we find .05 (on the "two-tails" line) on the top of our table and follow that column down to the row that corresponds to 60 degrees of freedom, we see that the critical statistic is 2.000.

Fourth, we finally get to calculate our test statistic. The formula for calculating a t statistic is as follows:

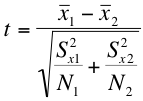
It's not as bad as it looks, I promise. If we plug in the means, variances and sample sizes of our example, it looks something like this:

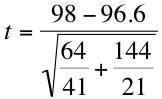
If we work that out, we get t = 1.4/2.9, which yields a t statistic of 0.48. But in order to make sense of that number, we need to compare it to our critical statistic, 2.000, which we can find on the cute little table your instructor gave you (see the end of Step 3 above for a more detailed explanation). Finally, we state our conclusion. Because our obtained t statistic (0.48) is smaller than the critical statistic (2.000), we accept the null hypothesis (or fail to reject the null hypothesis, as they say in the business) that the mean scores of men and women are the same. With a larger sample size, the standard error would have been smaller, so the t statistic would have been bigger and we would have had a better chance of rejecting the null hypothesis.

Main Points

• The t distribution is actually a family of distributions whose shapes vary according to their respective degrees of freedom, which is closely related to sample size.
• Hypothesis testing is a process by which we determine whether or not a sample result is likely to have occurred by chance. This process has five steps: (1) making assumptions (2) stating the null and research hypotheses and choosing an alpha level (3) selecting a sampling distribution and determining the test statistic that corresponds with the chosen alpha level (4) calculating the test statistic and (5) interpreting the results.
• We can use hypothesis tests to compare the mean of a sample to a known population mean (sometimes referred to as one-group hypothesis testing) and to compare two sample means (sometimes referred to as two-group hypothesis testing). Both types of hypothesis tests follow essentially the same process, but the formula used to calculate the test statistic differs between the two.

Hypothesis Testing in SPSS

To run a T-test in SPSS, click "Analyze," "Compare Means" and then "Independent-Samples T Test." The variable you want to test will go in the "Test Variable" space, and the "Grouping Variable" is how you define your two samples. For example, if you were testing the difference in income between men and women, income would go in the "Test Variable" box, and gender would go in the "Grouping Variable" box.

Once you have a variable to test in the "Test Variable" box and another in the "Grouping Variable" box, you'll need to click "Define Groups." (Note: the stage at which you define the groups you are going to test is where the vast majority of students get lost. So take your time with this next section.) Defining groups is necessary because T-tests can only handle two groups at once. If your grouping variable has more than two groups, you'll need to specify which two groups you would like to test. The "RACE" variable in the ADD Health dataset, for example, has five groups (White, African American, Native American, Asian/Pacific Islander and Other). If you wanted to use "RACE" as a grouping variable, you would need to tell SPSS which two groups to test (i.e., whites and African Americans, Native Americans and Others or maybe African Americans and Asians/Pacific Islanders—you get the idea). You cannot use a T-test to test all five groups at once.

Okay, now that we've got the "why" out of the way, lets move on to the "how." Suppose you wanted to use the ADD Health dataset to test for a difference in mean income between White and African American respondents. Many students begin by trying to type "White" into the "Group 1" box. When that doesn't work, they give up. Here's the thing: the "Group 1" and "Group 2" boxes will only accept numerical values. You need to enter the numbers that correspond to "White" and "African American." Go to the "Variable View" tab, and click on the "Value Labels" box for "RACE." You'll see that Whites were coded as ones and African Americans were coded as twos. That's what needs to go in the "Group 1" and "Group 2" boxes. So put a "1" for Whites in the "Group 1" box and a "2" for African Americans in the "Group 2" box and click "Continue." Similarly, if you wanted to test Whites and Asians/Pacific Islanders you would put a "1" in the "Group 1" box and a "4" in the "Group 2" box (Asians/Pacific Islanders were coded as fours). For an explanation of the SPSS output, I suggest you watch this video walkthrough:

Exercises

1. Using the NIS data, test for a difference in religious service attendance "ATTEND" between respondents who are married and those who have never been married (Hint: you'll need to check the value labels to see which number corresponds to each category). Report both the obtained statistic and the p-value. What is your conclusion? Does there appear to be a statistically significant difference?
2. Using the same dataset, test for a difference in "EDUCATION" between men and women (Again, you'll need to check the value labels to see how males and females are coded). Report both the obtained statistic and the p-value. What is your conclusion? Does there appear to be a statistically significant difference?