The Chi-Square Test for Independence

Learning Objectives

1. Understand the characteristics of the chi-square distribution
2. Carry out the chi-square test and interpret its results
3. Understand the limitations of the chi-square test

Key Terms

Chi-Square Distribution: a family asymmetrical, positively skewed distributions, the exact shape of which is determined by their respective degrees of freedom
Observed Frequencies: the cell frequencies actually observed in a bivariate table
Expected Frequencies: The cell frequencies that one might expect to see in a bivariate table if the two variables were statistically independent

Overview

The primary use of the chi-square test is to examine whether two variables are independent or not. What does it mean to be independent, in this sense? It means that the two factors are not related. Typically in social science research, we're interested in finding factors that are dependent upon each other—education and income, occupation and prestige, age and voting behavior. By ruling out independence of the two variables, the chi-square can be used to assess whether two variables are, in fact, dependent or not. More generally, we say that one variable is "not correlated with" or "independent of" the other if an increase in one variable is not associated with an increase in the another. If two variables are correlated, their values tend to move together, either in the same or in the opposite direction. Chi-square examines a special kind of correlation: that between two nominal variables.

The Chi-Square Distribution

The chi-square distribution, like the t distribution, is actually a series of distributions, the exact shape of which varies according to their degrees of freedom. Unlike the t distribution, however, the chi-square distribution is asymmetrical, positively skewed and never approaches normality. The graph below illustrates how the shape of the chi-square distribution changes as the degrees of freedom (k) increase:

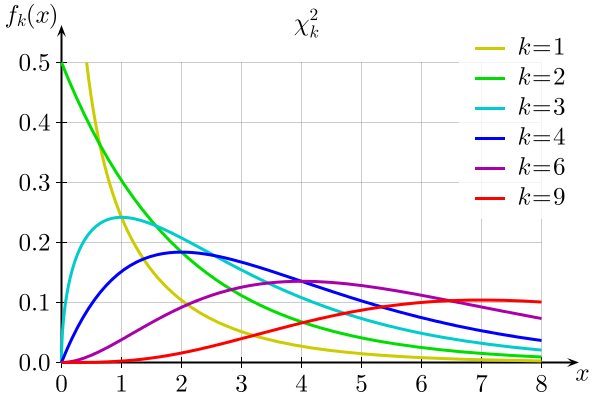
The Chi-Square Test

Earlier in the semester, you familiarized yourself with the five steps of hypothesis testing: (1) making assumptions (2) stating the null and research hypotheses and choosing an alpha level (3) selecting a sampling distribution and determining the test statistic that corresponds with the chosen alpha level (4) calculating the test statistic and (5) interpreting the results. Like the t tests we discussed previously, the chi-square test begins with a handful of assumptions, a pair of hypotheses, a sampling distribution and an alpha level and ends with a conclusion obtained via comparison of an obtained statistic with a critical statistic. The assumptions associated with the chi-square test are fairly straightforward: the data at hand must have been randomly selected (to minimize potential biases) and the variables in question must be nominal or ordinal (there are other methods to test the statistical independence of interval/ratio variables; these methods will be discussed in subsequent chapters). Regarding the hypotheses to be tested, all chi-square tests have the same general null and research hypotheses. The null hypothesis states that there is no relationship between the two variables, while the research hypothesis states that there is a relationship between the two variables. The test statistic follows a chi-square distribution, and the conclusion depends on whether or not our obtained statistic is greater that the critical statistic at our chosen alpha level.

In the following example, we'll use a chi-square test to determine whether there is a relationship between gender and getting in trouble at school (both nominal variables). Below is the table documenting the raw scores of boys and girls and their respective behavior issues (or lack thereof):

Gender and Getting in Trouble at School

	Got in Trouble	Did Not Get in Trouble	Total
Boys	46	71	117
Girls	37	83	120
Total	83	154	237

To examine statistically whether boys got in trouble in school more often, we need to frame the question in terms of hypotheses. The null hypothesis is that the two variables are independent (i.e. no relationship or correlation) and the research hypothesis is that the two variables are related. In this case, the specific hypotheses are:

H0: There is no relationship between gender and getting in trouble at school
H1: There is a relationship between gender and getting in trouble at school

As is customary in the social sciences, we'll set our alpha level at 0.05

Next we need to calculate the expected frequency for each cell. These values represent what we would expect to see if there really were no relationship between the two variables. We calculate the expected frequency for each cell by multiplying the row total by the column total and dividing by the total number of observations. To get the expected count for the upper right cell, we would multiply the row total (117) by the column total (83) and divide by the total number of observations (237). (83 x 117)/237 = 40.97. If the two variables were independent, we would expect 40.97 boys to get in trouble. Or, to put it another way, if there were no relationship between the two variables, we would expect to see the number of students who got in trouble be evenly distributed across both genders.

We do the same thing for the other three cells and end up with the following expected counts (in parentheses next to each raw score):

Gender and Getting in Trouble at School

	Got in Trouble	Did Not Get in Trouble	Total
Boys	46 (40.97)	71 (76.02)	117
Girls	37 (42.03)	83 (77.97)	120
Total	83	154	237

With these sets of figures, we calculate the chi-square statistic as follows:

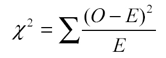
For each cell, we square the difference between the observed frequency and the expected frequency (observed frequency – expected frequency) and divide that number by the expected frequency. Then we add all of the terms (there will be four, one for each cell) together, like so:

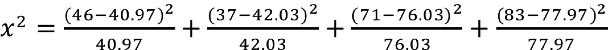
After we've crunched all those numbers, we end up with an obtained statistic of 1.87. (Please note: a chi-square statistic can't be negative because nominal variables don't have directionality. If your obtained statistic turns out to be negative, you might want to check your math.) But before we can come to a conclusion, we need to find our critical statistic, which entails finding our degrees of freedom. In this case, the number of degrees of freedom is equal to the number of columns in the table minus one multiplied by the number of rows in the table minus one, or (r-1)(c-1). In our case, we have (2-1)(2-1), or one degree of freedom.

Finally, we compare our obtained statistic to our critical statistic found on the chi-square table posted in the "Files" section on Canvas. We also need to reference our alpha, which we set at .05. As you can see, the critical statistic for an alpha level of 0.05 and one degree of freedom is 3.841, which is larger than our obtained statistic of 1.87. Because the critical statistic is greater than our obtained statistic, we can't reject our null hypothesis.

The Limitations of the Chi-Square Test

There are two limitations to the chi-square test about which you should be aware. First, the chi-square test is very sensitive to sample size. With a large enough sample, even trivial relationships can appear to be statistically significant. When using the chi-square test, you should keep in mind that "statistically significant" doesn't necessarily mean "meaningful." Second, remember that the chi-square can only tell us whether two variables are related to one another. It does not necessarily imply that one variable has any causal effect on the other. In order to establish causality, a more detailed analysis would be required.

Main Points

• The chi-square distribution is actually a series of distributions that vary in shape according to their degrees of freedom.
• The chi-square test is a hypothesis test designed to test for a statistically significant relationship between nominal and ordinal variables organized in a bivariate table. In other words, it tells us whether two variables are independent of one another.
• The obtained chi-square statistic essentially summarizes the difference between the frequencies actually observed in a bivariate table and the frequencies we would expect to see if there were no relationship between the two variables.
• The chi-square test is sensitive to sample size.
• The chi-square test cannot establish a causal relationship between two variables.

Carrying out the Chi-Square Test in SPSS

To perform a chi square test with SPSS, click "Analyze," then "Descriptive Statistics," and then "Crosstabs." As was the case in the last chapter, the independent variable should be placed in the "Columns" box, and the dependent variable should be placed in the "Rows" box. Now click on "Statistics" and check the box next to "Chi-Square." This test will provide evidence either in favor of or against the statistical independence of two variables, but it won't give you any information about the strength or direction of the relationship.

After looking at the output, some of you are probably wondering why SPSS provides you with a two-tailed p-value when chi-square is always a one-tailed test. In all honesty, I don't know the answer to that question. However, all is not lost. Because two-tailed tests are always more conservative than one-tailed tests (i.e., it's harder to reject your null hypothesis with a two-tailed test than it is with a one-tailed test), a statistically significant result under a two-tailed assumption would also be significant under a one-tailed assumption. If you're highly motivated, you can compare the obtained statistic from your output to the critical statistic found on a chi-square chart. Here's a video walkthrough with a slightly more detailed explanation:

Exercises

1. Using the World Values Survey data, run a chi-square test to determine whether there is a relationship between sex ("SEX") and marital status ("MARITAL"). Report the obtained statistic and the p-value from your output. What is your conclusion?
2. Using the ADD Health data, run a chi-square test to determine whether there is a relationship between the respondent's gender ("GENDER") and his or her grade in math ("MATH"). Again, report the obtained statistic and the p-value from your output. What is your conclusion?