Confidence Intervals

Learning Objectives

1. Understand the concept of estimation and why it is necessary
2. Calculate confidence intervals for proportions and means
3. Understand the concept of error and how to reduce it

Key Terms

Confidence Interval (Interval Estimate): A range of values defined by the confidence level within which the population parameter is estimated to fall
Confidence Level: The likelihood, expressed as a percentage or a probability, that a specified interval will contain the population parameter
Sampling Error: The discrepancy between a given sample statistic and its corresponding population parameter

Overview

Let's say we want to estimate the average commuting time (the average number of hours spent commuting each week) for students at the U. Because interviewing all 30,000 people on campus would be nearly impossible, we take a sample of 400. The following statistics are derived from our sample:

Sample = 400
Sample Mean = 10
Standard Deviation = 2

The sample mean is what's known as a point estimate. Point estimates are convenient and easy to calculate, but they're not terribly accurate. We suspect our sample mean (a sample statistic) is pretty close to the population parameter, but we don't know exactly how close because of sampling error. Here's the thing: samples vary. If we took 10 different samples of 400 students, each sample would probably give us a slightly different mean. They'd all be pretty close—and they'd be pretty close to the population parameter—but they'd still be different. This discrepancy between a given sample estimate and the corresponding population parameter is called sampling error.

To help manage the uncertainty created by sampling error, we use interval estimates. Rather than saying that the mean of a population is a certain number, we generally say that the mean of a population probably falls somewhere between two numbers. So for our example, rather than saying that the mean commute time is ten hours, we could say that it probably falls between nine and 11 hours.

In other words, an interval estimate is a range in which the population parameter probably falls for a given level of confidence. We have to establish a level of confidence because we can never be 100 percent sure that the population mean falls within our confidence interval.

Calculating Confidence Intervals for Means

Let's go back to our example of commute times for University of Utah students. Suppose we want to construct a 95 percent confidence interval for the mean commute time of our population. We would use the following formula:

In other words, the confidence interval for a mean is equal to the mean plus AND minus the product of the appropriate z score and the standard error of the sampling distribution. We find the appropriate z score for a given confidence interval by determining which z score will divide the sampling distribution in such a way that a certain percent of the area (based on your level of confidence) falls between the two points. The most common confidence intervals are 95 and 99, which give us z scores of 1.96 and 2.58, respectively. In other words, a z score of 1.96 divides the sampling distribution in such a way that 95 percent of the area under the curve (and, by extension, 95 percent of all possible sample means) fall between 1.96 and -1.96. Similarly, 99 percent of all possible sample means fall between 2.58 and -2.58.

We can use the following formula to find the standard error:

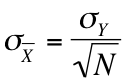
In layman's terms, the standard error is equal to our sample mean divided by the square root of the number of observations in our sample. So for our example, we could calculate a 95 percent confidence interval by plugging the appropriate numbers into the aforementioned equation.

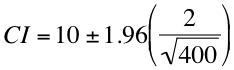
If we simplify that a little bit, we get the following two equations:

10 + 1.96(2/20) = 10.19
10 - 1.96(2/20) = 9.81

Our confidence interval would therefore be 10.19, 9.81. We could say that we're 95 percent sure that mean commute time for a student at the U is between 9.81 and 10.19 hours per week.

Calculating Confidence Intervals for Proportions

We can also calculate confidence intervals for proportions (aka percentages). Suppose we took a poll of 100 doomsday preppers and found that 55 percent of them were most concerned about the sudden, widespread outbreak of an incurable and deadly disease. We can construct a 95 percent confidence interval to see, based on our sample, what percent of doomsday preppers are most concerned about the emergence of such a disease.

Confidence intervals for proportions use the same general formula as those for means (the point estimate plus and minus the product of the appropriate z score and the standard error), but because we're using a proportion instead of a mean, the method we use to calculate the standard error is different. We still set it up like this:

But now we find the standard error by plugging our numbers into the following formula:

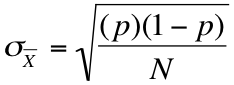
For our doomsday prepper example, the equation for a 95 percent confidence interval would look like this:

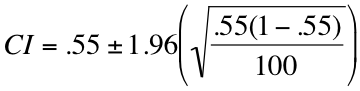
If we simplify that a bit, we get the following two equations:

0.55 + 1.96(0.05) = 0.65
0.55 – 1.96(0.05) = 0.45

Our 95 percent confidence interval is 0.65, 0.45. Or we could say that we're 95 percent sure that the true percentage of doomsday preppers who are primarily concerned about the sudden arrival of a deadly pandemic falls between 45 and 65 percent. Unfortunately, that confidence interval is too wide to be of much help. We could make it smaller either by taking a larger sample (i.e. surveying more doomsday preppers) or lowering our confidence level, both of which would yield a narrower confidence interval, albeit in different ways. Surveying more doomsday preppers would make the standard error smaller, which in turn would lead to a narrower confidence interval. Using a lower confidence level (i.e., 90 percent instead of 95 percent) would also shrink the width of the interval by contributing a smaller z score to the equation. In the social sciences, we don't often use a 99 percent confidence level because it makes the confidence interval too wide to be meaningful.

Main Points

• The goal of most research is to find population parameters. Because population parameters are notoriously difficult to ascertain, we usually have to estimate them.
• Confidence intervals can be used to estimate population parameters including means and proportions. Their accuracy is defined within the context of a confidence interval, the most common of which include 90 percent, 95 percent and 99 percent. In the social sciences, we usually use a 95 percent confidence interval.
• The two factors that determine the width of a confidence interval are sample size and confidence level. The size of the sample is inversely related to the width of the confidence interval. In other words, the larger the sample is, the smaller the confidence interval will be. The confidence level, in contrast, is directly related to the width of the confidence level. A higher confidence level (i.e., 99 percent instead of 95 percent) will make the confidence interval wider.

Calculating Confidence Intervals in SPSS

To calculate a confidence interval, click "Analyze," "Descriptive Statistics," then "Explore." Put the variables for which you would like to generate confidence intervals in the "Dependent list" space. If you put a control variable in the "Factor list" space, you will get confidence intervals for the right variable. To change the level of confidence (i.e., from 95% to 99% or vice versa), click "Statistics." This dialog box will open. The default level of confidence is 95%. Simply put a new number in the space to change the level of confidence. Here's a video walkthrough:

Exercises

1. Using the NIS dataset, create a 95% confidence interval for "INCOME." If you were to create a 99% confidence interval for "INCOME" would it be wider or narrower than the one you just generated? Why?
2. Still using the NIS dataset, create a 99% confidence level for "EDUCATION." Now factor by "VISACAT." How do the confidence intervals generated for each of the five visa categories differ from the one generated using the entire sample? Do any of the subgroups stand out in terms of educational attainment (or lack thereof)?